Gsscsd
文章 标签 分类 关于
Gsscsd

目录

从word2vec到negative sampling

 收录于 深度学习
   约 6349 字   预计阅读 13 分钟    次阅读  

到目前为止，word2vec算法不单单是nlp的基础，也成为推荐和搜索的基础，本文记录一下word2vec算法中的negative sampling方案，并基于此记录了其他的sampling方法。

参考链接：

Skip-gram方法的word2vec

在word2vec出现之前，已经有用神经网络DNN来用训练词向量进而处理词与词之间的关系了。采用的方法一般是一个三层的神经网络结构（当然也可以多层），分为输入层，隐藏层和输出层(softmax层)。

这个模型是如何定义数据的输入和输出呢？一般分为CBOW(Continuous Bag-of-Words 与Skip-Gram两种模型。

CBOW模型的训练输入是某一个特征词的上下文相关的词对应的词向量，而输出就是这特定的一个词的词向量。

Skip-Gram模型和CBOW的思路是反着来的，即输入是特定的一个词的词向量，而输出是特定词对应的上下文词向量。

PS：skip-gram 出来的准确率比cbow 高，cbow比sg训练快，sg比cbow更好地处理生僻字（出现频率低的字）。

在词向量训练任务中，softmax函数有如下：

$$p(w|c) = \frac{\exp(h^\top v_w)}{\sum_{w_i \in V} \exp(h^\top v_{w_i})}=\frac{\exp(h^\top v_w)}{Z(h)}$$

其中，$h$是隐藏层的输出， $v_{w_i}$是w对应的输出词向量（即softmax的权重矩阵）,$V$是词典，$c$是上下文。

在神经网络语言模型中，一般会把$C$压缩为$h$。 从上面的公式可以看出，softmax函数的分母是对所有词典进行遍历求和，当$V$的size比较小的时候，softmax的求导以及梯度下降速度较快，但是当$V$的size比较大的时候，softmax的分母需要遍历所有的样本进行求和，因此速度较慢，对于此问题，业界提出了多种方法来解决该问题，常见的方法有Noise Contrastive Estimation(NCE)，negative sampling，sampling softmx算法等，接下来分别讲解一下两种算法。

Noise Contrastive Estimation算法

对于每一个训练样本（x, T)，我们训练binary classification，而不是multiclass classification。具体一点，我们对于每个样本，拆分成一个真实的（x,y) pair,另外我们随机产生k个Noise的（x,y）pair,这样我们就可以用来训练处这样的binary classifier。

用概率来表示，这个问题由之前的P(y|x) 通过x预测所有y，换成了P(x,y)，计算x,y同时存在的概率，换言之，从基于特征x求y的最大后验概率，变成基于特征X和y，共同出现的最大后验概率。

假设共有m个样$(l_i,c_i)$, 建模: \begin{equation} P\left(l_{i} \mid c_{i}\right)=\frac{u_{\theta}\left(l_{i}, c_{i}\right)}{\sum_{i}^{n} u_{\theta}\left(l_{j}, c_{i}\right)}=\frac{u_{\theta}\left(l_{i}, c_{i}\right)}{Z_{i}} \end{equation} 假设负例label从某个分布$Q(l_i)$中抽取, 且抽取$k$次. 正例从上面的分布抽取, 则有: $(l_i,c_i)$真实样本的概率： \begin{equation} P\left(\text { True } \mid l_{i}, c_{i}\right)=\frac{P\left(l_{i} \mid c_{i}\right)}{k Q\left(l_{i}\right)+P\left(l_{i} \mid c_{i}\right)}=P\left(T \mid l_{i}, c_{i}\right) \end{equation} $(l_i,c_i)$负样本的概率： \begin{equation} P\left(\text { False } \mid l_{i}, c_{i}\right)=\frac{k Q\left(c_{i}\right)}{k Q\left(l_{i}\right)+P\left(l_{i} \mid c_{i}\right)}=P\left(F \mid l_{i}, c_{i}\right) \end{equation} 最终最大化log似然估计, 损失函数: \begin{equation} J(\theta) = \prod_{(w,c) \in T} P(T|w,c;\theta) \prod_{(w,c) \in Neg} P(F|w,c;\theta) \end{equation} \begin{equation} L=\sum_{i}^{n}\left(\log P\left(T \mid l_{i}, c_{i}\right)+k \sum_{i=0, L_{x} \sim Q\left(l_{i}\right)}^{k} \log P\left(F \mid L_{x}, c_{i}\right)\right) \end{equation}

negative sampling算法

负采样Negative Sampling是NCE的一个变种，概率的定义有所区别。

建模, 作为二分类softmax损失. \begin{equation} P\left(T \mid l_{i}, c_{i}\right)=\frac{u_{\theta}\left(l_{i}, c_{i}\right)}{1+u_{\theta}\left(l_{i}, c_{i}\right)}=\sigma\left(u_{\theta}\left(l_{i}, c_{i}\right)\right) \end{equation} \begin{equation} P\left(F \mid l_{i}, c_{i}\right)=1-P\left(T \mid l_{i}, c_{i}\right)=\frac{1}{1+u_{\theta}\left(l_{i}, c_{i}\right)}=1-\sigma\left(u_{\theta}\left(l_{i}, c_{i}\right)\right) \end{equation}

最终最大化log似然估计略(和NCE相同), 负例的采样时, 为全体样本的所有$l$不消重的均匀采样,或者每个$l$采到的概率为: \begin{equation} P\left(l_{x}\right)=\frac{\operatorname{cnt}\left(l_{x}\right)^{0.75}}{\sum_{y \in L} \operatorname{cnt}\left(l_{y}\right)^{0.75}} \end{equation}

注意，构造样本时，要注意正负样本的比例，如果考虑所有的负样本，会导致正负比例失衡，模型权重会被负样本带偏。

sampling softmax算法(sampled_softmax_loss)

Sampled softmax方法不同于nce方法，nce是把多分类问题转化成二分类，而sampled softmax方法则是只抽取一部分样本计算softmax。训练的时候不需要特别精准的softmax归一化概率，只需要一个粗略值做back propoagation就好了。这么粗糙的算法，可能会导致分布不一致问题？？？

如果损失函数采用交叉熵损失函数: \begin{equation} H(q,p) = - \sum_x q(x) \log p(x) \end{equation}

这里q是真实期望分布,例如 $q=[0,…1,…,0]$，p是模型输出分布，对应最上面的softmax公式。

对于一个样本，可得交叉熵损失函数(这里把模型的参数统称为$\theta$): \begin{equation} J_\theta = - \text{log} \dfrac{\text{exp}({h^\top v_{w}})}{\sum_{w_i \in V} \text{exp}({h^\top v_{w_i}})} \end{equation} 假设：$\mathcal{E}(w)=-h^\top v_{w}$, 则： \begin{equation} J_\theta = \mathcal{E}(w) + \text{log} \sum_{w_i \in V} \text{exp}( - \mathcal{E}(w_i)) \end{equation} 对$\theta$求梯度得： \begin{equation} \nabla_\theta J_\theta = \nabla_\theta \mathcal{E}(w) + \sum_{w_i \in V} \dfrac{\text{exp}(- \mathcal{E}(w_i))}{\sum_{w_i \in V} \text{exp}(- \mathcal{E}(w_i))} \nabla_\theta (- \mathcal{E}(w_i)) \end{equation} 已知：$p(w_i) = \dfrac{\text{exp}(- \mathcal{E}(w_i))}{\sum_{w_i \in V} \text{exp}- \mathcal{E}(w_i))}$, \begin{equation} \nabla_\theta J_\theta = \nabla_\theta \mathcal{E}(w) - \sum_{w_i \in V} P(w_i) \nabla_\theta (\mathcal{E}(w_i)) \end{equation}

对于梯度公式的第二部分，可以认为是$\nabla_\theta (\mathcal{E}(w_i))$对于softmax输出$P(w_i)$的期望，即： \begin{equation} \sum_{w_i \in V} P(w_i) \nabla_\theta \mathcal{E}(w_i) = \mathbb{E}{w_i \sim P}[\nabla\theta \mathcal{E}(w_i)] \end{equation} 上面的这个公式就是控制softmax采样需要优化的部分。

根据传统的重要性采样方法，按照如下公式计算期望： \begin{equation} \frac{1}{N} \sum_{w_i \sim Q(w)}\frac{P(w_i)}{Q(w_i)}\nabla_\theta \mathcal{E}(w_i) \approx \mathbb{E}{w_i \sim P}[\nabla\theta \mathcal{E}(w_i)] \end{equation} 其中$N$是从分布$Q$(我们自己定义的一个容易采样的分布)中采样的样本数，但是这种方法仍然需要计算$P(wi)$，而$P(wi)$的计算又需要softmax做归一化，这是我们不想看到的，所以要使用一种有偏估计的方法。

Softmax公式的分母部分： \begin{equation} Z(h)=\sum_{w_i \in V} \text{exp}(- \mathcal{E}(w_i))=M\sum_{w_i \in V} (\frac{1}{M})\cdot \text{exp}(- \mathcal{E}(w_i)) \end{equation} 公式中$\sum_{w_i \in V} (\frac{1}{M})\cdot \text{exp}(- \mathcal{E}(w_i))$是一种期望形式，因而可以通过采样方法进行估计得到$Z(h)$, 对于$Z(h)$的采样候选分布仍旧选择$Q$分布。 则可以得到： \begin{equation} Z(h)=\hat{Z}(h)=\frac{M}{N}\sum_{w_i \sim Q(w)}\frac{\hat{R}(w_i)\text{exp}(- \mathcal{E}(w_i))}{Q(w_i)}=\frac{M}{N}\sum_{w_i \sim Q(w)}\frac{\text{exp}(- \mathcal{E}(w_i))}{M\cdot Q(w_i)} \end{equation} 上式中的$\hat{R}(w_i)$代表概率$\frac{1}{M}$，约去$M$可得： \begin{equation} \hat{Z}(h)=\frac{1}{N}\sum_{w_i \sim Q(w)}\frac{\text{exp}(- \mathcal{E}(w_i))}{ Q(w_i)} \end{equation} 到这里，我们就可以用$\hat{Z}(h)$去近似$Z(h)$了。

现在理一下思路：给定候选分布Q，传统采样方法需要计算P，也就是说需要计算分母Z，这是我们不想看到的。幸运的是分母Z仍然可以通过采样得到，采样Z的时候，仍然采用候选分布Q。

\begin{equation} \frac{1}{N} \sum_{w_i \sim Q(w)}\frac{P(w_i)}{Q(w_i)} \nabla \theta \mathcal{E}(w_i) \approx \mathbb{E}{w_i \sim P}[\nabla _\theta \mathcal{E}(w_i)] \end{equation}

\begin{equation} \frac{1}{N}\sum_{w_i \sim Q(w)}\frac{\hat{P}(w_i)}{Q(w_i)}\nabla \theta \mathcal{E}(w_i) \approx \mathbb{E}{w_i \sim P}[\nabla \theta \mathcal{E}(w_i)] \end{equation} 其中 $\hat{P}(wi)$代表采样方式获得的概率： \begin{equation} \hat{P}(w_i)=\frac{\text{exp}(- \mathcal{E}(w_i))}{\hat{Z}(h)} \end{equation} 可得： \begin{equation} \mathbb{E}{w_i \sim P}[\nabla_\theta \mathcal{E}(w_i)]\approx \frac{1}{N}\sum_{w_i \sim Q(w)}\frac{\text{exp}(- \mathcal{E}(w_i))}{Q(w_i)\hat{Z}(h)}\nabla_\theta \mathcal{E}(w_i) \end{equation} 现在我们就从$Q$分布中采样$N$个样本，组成集合$J$，最终得到： \begin{equation} \mathbb{E}{w_i \sim P}[\nabla\theta \mathcal{E}(w_i)]\approx \frac{\sum_{w_j \in J}\text{exp}(- \mathcal{E}(w_j))\nabla_\theta \mathcal{E}(w_j)/Q(w_j)}{\sum_{w_j \in J}\text{exp}(- \mathcal{E}(w_j))/Q(w_j)} \end{equation} 整体梯度为： \begin{equation} \nabla_\theta J_\theta = : \nabla_\theta \mathcal{E}(w) - \frac{\sum_{w_j \in J}\text{exp}(- \mathcal{E}(w_j))\nabla_\theta \mathcal{E}(w_j)/Q(w_j)}{\sum_{w_j \in J}\text{exp}(- \mathcal{E}(w_j))/Q(w_j)} \end{equation}

Tensorflow的采样方法：candidate sampling

假如我们有一个多分类任务或者多标签分类任务，给定训练集$(x_i,T_i)$，其中xixi表示上下文，$T_i$表示目标类别(可能有多个).可以用word2vec中的negtive sampling方法来举例，使用cbow方法，也就是使用上下文$x_i$来预测中心词(单个target$T_i$)，或者使用skip-gram方法，也就是使用中心词$x_i$来预测上下文(多个target($T_i$)).

我们想学习到一个通用函数$F(x,y)$来表征上下文$x$和目标类$y$的关系，如Word2vec里面，使用上下文预测下个单词的概率。

完整的训练方法，如使用softmax或者Logistic回归需要对每个训练数据计算所有类$y\in L$的概率$F(x,y)$，当$|L|$非常大的时候，训练将非常耗时。

“candidate sampling"训练方法包括为每一个训练数据$(x_i,T_i)$构造一个训练任务，使得我们只需要使用一个较小的候选集合$C_i\in L$，就能评估$F(x,y)$,典型的，candidate set $C_i$包含目标类别$T_i$和一些随机采样的类别$S_i\in L$：$C_i = T_i \cup S_i$ , $S_i$的选择可能依赖 $x_i$和 $T_i$，也可能不依赖。 $F(x,y)$可以使用神经网络计算来表征(也就是TensorFlow里面常用的logits)

https://img-blog.csdn.net/20170410171426202?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvdTAxMDIyMzc1MA==/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast 其中：

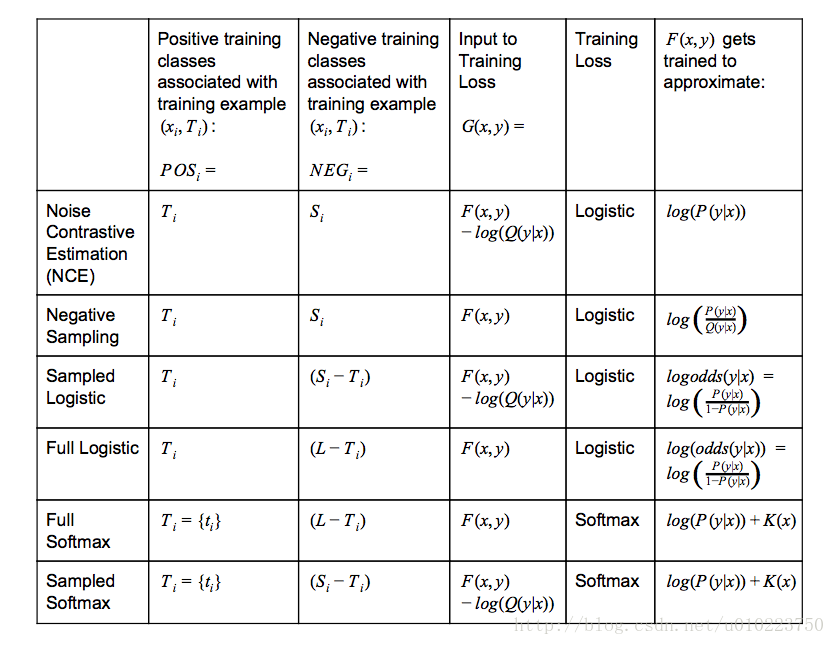
  • $Q(y|x)$表示的是给定context $x_i$采样到$y$的概率
  • $K(x)$表示任意不以来候选集的函数
  • $logistic-training-loss = \sum_{i}(\sum_{y \in POS_i} log(1+exp(-G(x_i,y)) )+\sum_{y \in NEG_i} log(1+exp(G(x_i,y)) ))$
  • $softmax-training-loss = \sum_{i}(-log(\frac{exp(G(x_i,t_i))}{\sum_{y \in POS_i \cup NEG_i} exp(G(x_i,y))}))$

在使用tensoflow的时候，我们有时候会纠结选择什么样的损失函数比较好，softmax和logistic在表达形式上是有点区别的，但是也不是很大，而且对于普通的softmax_cross_entropy_with_logits和sigmoid_cross_entropy_with_logits也都能够进行多分类任务，那么他们之间的区别是什么的？

就我个人所想到的，使用sigmoid_cross_entropy_with_logits和softmax_cross_entropy_with_logits的最大的区别是类别的排他性，在分类任务中，使用softmax_cross_entropy_with_logits我们一般是选择单个标签的分类，因为其具有排他性，说白了，softmax_cross_entropy_with_logits需要的是一个类别概率分布，其分布应该服从多项分布(也就是多项logistic regression)，我们训练是让结果尽量靠近这种概率分布，不是说softmax_cross_entropy_with_logits不能进行多分，事实上softmax_cross_entropy_with_logits是支持多个类别的，其参数labels也没有限制只使用一个类别，当使用softmax_cross_entropy_with_logits进行多分类时候，以二类为例，我们可以设置真实类别的对应labels上的位置是0.5,0.5，训练使得这个文本尽量倾向这种分布，在test阶段，可以选择两个计算概率最大的类作为类别标签，从这种角度说，使用softmax_cross_entropy_with_logits进行多分，实际上类似于计算文本的主题分布。

对于sigmoid_cross_entropy_with_logits，公式可以看出，sigmoid_cross_entropy_with_logits其实是训练出了多个分类器，对于有n个标签的分类问题，其实质是分成了n个二分类问题，这点和softmax_cross_entropy_with_logits有着本质的区别。

tensorflow提供了下面两种candidate sample方法

  • tf.nn.nce_loss
  • tf.nn.sampled_softmax_loss

tf.nn.nce_loss使用的是logistic, 而tf.nn.sampled_softmax_loss采用的是softmax loss，其实这两者的区别也主要在这儿，采用logistic loss的本质上还是训练n个分类器，而使用softmax loss的其实只是训练了一个主题分类器，tf.nn.nce_loss主要思路也是判断给定context $C_i$和训练数据$x_i$，判断每一个$y_i$是不是target label，而 tf.nn.sampled_softmax_loss则是使得在target label上的分布概率最大化。

对于多标签多类别的分类任务使用Logistic比较好，对于多标签单类别的分类任务使用softmax比较好，采样中，采用tf.nn.sampled_softmax_loss训练cbow模型比较好，而 tf.nn.nce_loss训练skip-gram比较好。

tensorflow 源码解析：

_compute_sampled_logits输入隐藏层输出和真标签，在里面采样获得S集，并计算，返回的就是F（x,y）-logQ，在nce_loss和sampled_softmax_loss中都调用它进行采样，详细的源码解释在下面

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

def sampled_softmax_loss(weights,
                         biases,
                         labels,
                         inputs,
                         num_sampled,
                         num_classes,
                         num_true=1,
                         sampled_values=None,
                         remove_accidental_hits=True,
                         partition_strategy="mod",
                         name="sampled_softmax_loss",
                         seed=None):
logits, labels = _compute_sampled_logits(
      weights=weights,
      biases=biases,
      labels=labels,
      inputs=inputs,
      num_sampled=num_sampled,
      num_classes=num_classes,
      num_true=num_true,
      sampled_values=sampled_values,
      subtract_log_q=True,
      remove_accidental_hits=remove_accidental_hits,
      partition_strategy=partition_strategy,
      name=name,
      seed=seed)
  labels = array_ops.stop_gradient(labels, name="labels_stop_gradient")
  sampled_losses = nn_ops.softmax_cross_entropy_with_logits_v2(
      labels=labels, logits=logits)
  # sampled_losses is a [batch_size] tensor.
  return sampled_losses

_compute_sampled_logits的参数和返回

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106

  Args:
    weights: A `Tensor` of shape `[num_classes, dim]`, or a list of `Tensor`
        objects whose concatenation along dimension 0 has shape
        [num_classes, dim].  The (possibly-sharded) class embeddings.
    biases: A `Tensor` of shape `[num_classes]`.  The class biases.
这里我用L指代所有的类别的集合，h指代隐藏层向量维度，这两个维度就是[L,h],[L]

weights biases就是我们的上下文embedding,你把embedding传进去，
他采样之后就用输出h和这个embedding相乘，只计算那些被采样的样品就可以了。
还有一个就是注意weights的shape,dim是在后面的
他在sampled_softmax_loss调用中也强调了，你训练的时候才用，像下面这样有个选择

if mode == "train":
  loss = tf.nn.sampled_softmax_loss(
      weights=weights,
      biases=biases,
      labels=labels,
      inputs=inputs,
      ...)
elif mode == "eval":
  logits = tf.matmul(inputs, tf.transpose(weights))
  logits = tf.nn.bias_add(logits, biases)
  labels_one_hot = tf.one_hot(labels, n_classes)
  loss = tf.nn.softmax_cross_entropy_with_logits(
      labels=labels_one_hot,
      logits=logits)
eval的时候乘法weights有一个transpose


    labels: A `Tensor` of type `int64` and shape `[batch_size,
        num_true]`. The target classes.  Note that this format differs from
        the `labels` argument of `nn.softmax_cross_entropy_with_logits`.
这里labels就是标签，他也提到了与上面eval的时候输入是不一样的，那个需要你进行一个one_hot
num_true如果我们用softmax就是1，其他的就是多标签
shape是[m,T],m是batch的大小

    inputs: A `Tensor` of shape `[batch_size, dim]`.  The forward
        activations of the input network.
这就是h 输出
[m,h]

    num_sampled: An `int`.  The number of classes to randomly sample per batch.
在这里可以看出，是一个批次，用同样的sampled的类，这个就是集合S的大小
用指代S

    num_classes: An `int`. The number of possible classes.
就是所有的类别，词表L的大小

    num_true: An `int`.  The number of target classes per training example.
用T指代
源码里有一个注意：
  Note: In the case where num_true > 1, 
we assign to each target class  the target probability 1 / num_true 
so that the target probabilities  sum to 1 per-example.
就是说如果有T个真目标类，那每个真类别的采样概率Q就是1/T,有点像上面文章里的1/|V|，
但这里我也有个疑问，如果我们是1个标签，那Q就是1了吗？但论文中也没提到正样本的Q怎么计算




    sampled_values: a tuple of (`sampled_candidates`, `true_expected_count`,
        `sampled_expected_count`) returned by a `*_candidate_sampler` function.
        (if None, we default to `log_uniform_candidate_sampler`)
这里如果none，函数会自己调用的log_uniform_candidate_sampler。
但如果你要用其他采样，你就得把采样后的结果是一个元组给他，格式我们也下面介绍。
其余采样方法这个我们下文再详细介绍。

    subtract_log_q: A `bool`.  whether to subtract the log expected count of
        the labels in the sample to get the logits of the true labels.
        Default is True.  Turn off for Negative Sampling.
是否减去logQ，按上面那个表格NCE和sampled softmax都要减的，负采样不减。



    remove_accidental_hits:  A `bool`.  whether to remove "accidental hits"
        where a sampled class equals one of the target classes.  Default is
        True.
如果采样到真标签了怎么办，是否删掉这次采样，默认是True要删掉
百度paddle里说如果为真，如果一个sample[i，j]意外地碰到了真标签，
那么相应的sampled_logits[i，j]将被减去1e20，使其SoftMax结果接近零。默认值为True。
框架多还是有好处的
https://www.paddlepaddle.org.cn/documentation/docs/zh/api_cn/layers_cn/sampled_softmax_with_cross_entropy_cn.html#sampled-softmax-with-cross-entropy

下面来自上面的博客https://narcissuscyn.github.io/2018/07/03/CandidateSampling/ 
其实两个loss的核心代码都是_compute_sampled_logits，但是在实现上不同的地方有两点：
sampled_softmax_loss是有去重的，也就是remove_accidental_hits=True,
但是nce_loss是不去重的，我们从上面的表也能看出来。
sampled_softmax_loss采用的是softmax+CE，但是nce_loss采用的是sigmod+CE


    partition_strategy: A string specifying the partitioning strategy, relevant
        if `len(weights) > 1`. Currently `"div"` and `"mod"` are supported.
        Default is `"mod"`. See `tf.nn.embedding_lookup` for more details.

    name: A name for the operation (optional).
    seed: random seed for candidate sampling. Default to None, which doesn't set
        the op-level random seed for candidate sampling.

  Returns:
    out_logits: `Tensor` object with shape
        `[batch_size, num_true + num_sampled]`, for passing to either
        `nn.sigmoid_cross_entropy_with_logits` (NCE) or
        `nn.softmax_cross_entropy_with_logits` (sampled softmax).
输出格式就是[m,T+S]
    out_labels: A Tensor object with the same shape as `out_logits`.
输出格式也是[m,T+S]
更新于 2021-03-13
 深度学习
返回 | 主页