从一个例子看机器学习

要想知道什么是机器学习，我们就需要首先理解机器是什么，机器就是电脑、芯片、代码这些东西。让电脑遵循人的指令，完成一件特定的任务从计算机发明那天开始就在研究了，现在的各种编程语言、数据结构和编程算法等都是在做这个。但是它们只能依赖于程序员输入的确定的代码才能 work，也就是说他们不能“自己学习”，这样对于有些问题就很尴尬，比如检测一张图片中有几个人，识别一句话中提到了几个人名，识别一张图片是不是黄图等等。这些任务要是写一个代码，依靠规则去实现，那还是非常困难。但是我们可以换个思路，让我们写代码去实现这些功能很困难，但是让我们去给图片打标签（比如给一批图，人为的打上是不是黄图的标签…）不是很简单的嘛，我们如果能让机器自己从打好标签的图片中自己学习那些是黄图不就万事大吉了嘛。这样看的话，标注的工作就对应了传统写代码中写规则匹配的工作。

那么有了标注好的图片，怎么让程序学习呢？这一步就需要借助于万能的数学了。如果我们能构造一个拟合函数，这个拟合函数可以拟合训练集，比如这里就是给函数输入各个图片的像素 RGB 值，输出就是是不是黄图。拟合完了之后给定一张没见过的图片也就能用这个函数得到是不是黄图了。

那么具体是怎么实现这个思路的呢？想一想最小二乘法的做法。举个例子，比如有 100 个点（x0,y0),...,(x100,y100），我们想用一条直线去拟合它。首先直线的方程就是$$y=ax+b$$, 其实这里我们只要求出 a 和 b 就行了，a 和 b 的选择有无数多种，我们要选一种最好的。没有量化就没有优化，我们首先要把 “最好的” 这个标准进行量化，在数学上就是选一个目标函数，比较好的一个目标函数就是让每个点到 y 的距离之和最小。 所以目标函数就是 $$\sum_{i=0}^{n}\frac{\left | ax_{i} - y_{i} + b \right |}{\sqrt{a^{2}+1}}$$，我们要让它最小。

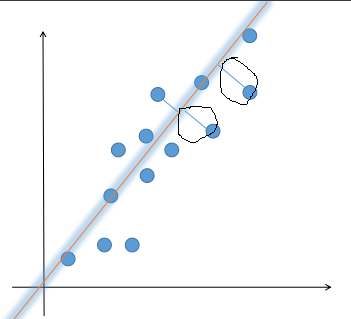
考虑到分母都是一样的，因此，我们在这里只关注距离，所以可以把一个点的误差写成$$ \left | x_{i}- (ax_{i}+b)\right |$$。然后把每个点的误差加起来就是我们的目标函数了。我们要让理论值和测试值之间误差最小，这样表示的目标函数就是$$\sum_{i=0}^{n}\left | x_{i}- (ax_{i}+b)\right |$$。

但是绝对值是个令人头痛的东西，是一个分段函数并且还有不可导的点。所以我们用平方代替，最终的目标函数是 $$\sum_{i=0}^{n} (x_{i}- (ax_{i}+b))^{2}$$，现在的任务只要求使得这个式子最小的 a 和 b 就行了。在高等数学中，对于这个问题只要对 a 和 b 分别求偏导，并令其为 0，然后解一个二元一次方程就行了。

上面例子的分析流程就是机器学习的步骤。其流程都是确定目标函数，然后对每个参数求导的方法找到目标函数的最大值（优化参数的过程）。只不过这里每个步骤都有很多方法可以选择。

针对是否有训练集：

• 有监督
• 无监督
• 半监督

目标函数：

• 极大似然估计
• 贝叶斯估计
• 平方误差
• 交叉熵

优化参数：

• 直接解析
• EM算法
• 牛顿法
• 梯度下降法