Gsscsd
文章 标签 分类 关于
Gsscsd

目录

python之Numpy学习笔记

 收录于 Python
   约 5004 字   预计阅读 10 分钟    次阅读  

NumPy 是一个 Python 包。 它代表 “Numeric Python”。 它是一个由多维数组对象和用于处理数组的例程集合组成的库。 Numeric，即 NumPy 的前身，是由 Jim Hugunin 开发的。 也开发了另一个包 Numarray ，它拥有一些额外的功能。 2005年，Travis Oliphant 通过将 Numarray 的功能集成到 Numeric 包中来创建 NumPy 包。 这个开源项目有很多贡献者。

Numpy 基础

NumPy的主要对象是同种元素的多维数组。这是一个所有的元素都是一种类型、通过一个正整数元组索引的元素表格(通常是元素是数字)。在NumPy中维度(dimensions)叫做轴(axes)，轴的个数叫做秩(rank)。

NumPy的数组类被称作ndarray。通常被称作数组。注意numpy.array和标准Python库类array.array并不相同，后者只处理一维数组和提供少量功能。更多重要ndarray对象属性有：

  • ndarray.ndim: 数组轴的个数，在python的世界中，轴的个数被称作秩
  • ndarray.shape:数组的维度。这是一个指示数组在每个维度上大小的整数元组。例如一个n排m列的矩阵，它的shape属性将是(2,3),这个元组的长度显然是秩，即维度或者ndim属性
  • ndarray.size 数组元素的总个数，等于shape属性中元组元素的乘积。
  • ndarray.dtype 一个用来描述数组中元素类型的对象，可以通过创造或指定dtype使用标准Python类型。另外NumPy提供它自己的数据类型。
  • ndarray.itemsize 数组中每个元素的字节大小。例如，一个元素类型为float64的数组itemsiz属性值为8(=64/8),又如，一个元素类型为complex32的数组item属性为4(=32/8).
  • ndarray.data 包含实际数组元素的缓冲区，通常我们不需要使用这个属性，因为我们总是通过索引来使用数组中的元素。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

import numpy as np 
a = np.arange(15).reshape(3, 5)
a
# array([[ 0,  1,  2,  3,  4],
#        [ 5,  6,  7,  8,  9],
#        [10, 11, 12, 13, 14]])
a.shape
#(3,5)
a.ndim
#2
a.dtype.name
#"int64"
a.itemsize
#8
a.size
#15
type(a)
#numpy.ndarray

创建数组

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

# 创建数组有多种方式
# 1.使用np.array(),将list转换成ndarray
import numpy as np 
a = np.array([2,3,4])
# 2. 数组将序列包含序列转化成二维的数组，序列包含序列包含序列转化成三维数组等等。
b = np.array( [ (1.5,2,3), (4,5,6) ] )
# array([[1.5, 2. , 3. ],
#        [4. , 5. , 6. ]])
#3. 使用占位符
# 通常，数组的元素开始都是未知的，但是它的大小已知。因此，NumPy提供了一些使用占位符创建数组的函数。这最小化了扩展数组的需要和高昂的运算代价。
# 函数 zeros创建一个全是0的数组，函数 ones创建一个全1的数组，函数 empty创建一个内容随机并且依赖与内存状态的数组。默认创建的数组类型(dtype)都是float64。
c = np.zeros( (3,4) )
d = np.ones( (3,4),dtype=int16)
# 4. 使用arrange函数 arange参数：(start,end,step)
e = np.arange( 10, 30, 5 )
# 5. 使用linspace生成指定元素 linspace参数: (start,end,num)
f = np.linspace(10,20,100)

基本运算

数组的算术运算是按元素的。新的数组被创建并且被结果填充。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import numpy as np 
a = np.array([20,30,40,50])
b = np.arange(4)
# 1. 基本运算
b + a
# array([20, 31, 42, 53])
a - b
#array([20, 29, 38, 47])
b**2
#array([0, 1, 4, 9])
a < 35
# array([ True,  True, False, False])
# ２.NumPy中的乘法运算符*指示按元素计算，矩阵乘法可以使用dot函数或创建矩阵对象实现
##  对应元素的乘法
A = np.array( [[1,1], [0,1]] )
# array([[1, 1],
#        [0, 1]])
B = np.array( [[2,0],[3,4]] )
# array([[2, 0],
#        [3, 4]])
A*B
#array([[2, 0],
#        [0, 4]])
# 3. 指定 axis参数,在指定的轴上进行计算
## axis :0代表行，1代表列
c = np.arange(12).reshape(3,4)
# array([[ 0,  1,  2,  3],
#        [ 4,  5,  6,  7],
#        [ 8,  9, 10, 11]])
c.sum(axis = 0)
# array([12, 15, 18, 21])
c.sum(axis = 1)
# array([ 6, 22, 38])

索引 切片 迭代

一维数组可以被索引、切片和迭代，就像列表和其它Python序列。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

import numpy as np 

# 多维数组可以每个轴有一个索引。这些索引由一个逗号分割的元组给出。
a = np.arange(15).reshape(3, 5)
a
# array([[ 0,  1,  2,  3,  4],
#        [ 5,  6,  7,  8,  9],
#        [10, 11, 12, 13, 14]])
a[0,0]
# 0
# 第一行
a[0,:]
# array([0, 1, 2, 3, 4])
# 第一列
a[:,0]
#array([ 0,  5, 10])

形状操作

一个数组的形状可以被多种命令修改

  • flatten
  • ravel
  • transpose
  • reshape

由 ravel()展平的数组元素的顺序通常是“C风格”的，就是说，最右边的索引变化得最快，所以元素a[0,0]之后是a[0,1]。如果数组被改变形状(reshape)成其它形状，数组仍然是“C风格”的。NumPy通常创建一个以这个顺序保存数据的数组，所以 ravel()将总是不需要复制它的参数3。但是如果数组是通过切片其它数组或有不同寻常的选项时，它可能需要被复制。函数 reshape()和 ravel()还可以被同过一些可选参数构建成FORTRAN风格的数组，即最左边的索引变化最快。 reshape函数改变参数形状并返回它，而resize函数改变数组自身。

如果在改变形状操作中一个维度被给做-1，其维度将自动被计算

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

import numpy as np 

# 生成一个二维的数据
a = np.floor(10*np.random.random((3,4)))
# array([[5., 3., 7., 2.],
#        [6., 7., 7., 0.],
#        [1., 9., 9., 0.]])
a.shape
# (3,4)
a.ravel() # 展成一维数组
# array([5., 3., 7., 2., 6., 7., 7., 0., 1., 9., 9., 0.])
a.flatten()
# array([5., 3., 7., 2., 6., 7., 7., 0., 1., 9., 9., 0.])
a.transpose()  # 等于a.T
# array([[5., 6., 1.],
#        [3., 7., 9.],
#        [7., 7., 9.],
#        [2., 0., 0.]])
# 更改自身维度
a.resize((2,6))
a.shape
# (2, 6)

组合(stack)不同的数组

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

import numpy as np 
a = np.floor(10*np.random.random((2,2)))
# array([[0., 9.],
#        [3., 4.]])
b = np.floor(10*np.random.random((2,2)))
# array([[4., 5.],
#        [2., 5.]])
## vstack 垂直排列 等于 np.concatenate([a,b],axis = 0)
np.vstack((a,b))
# array([[0., 9.],
#        [3., 4.],
#        [4., 5.],
#        [2., 5.]])
## hstack 水平排列 等于 np.concatenate([a,b],axis = 1)
np.hstack([a,b])
# array([[0., 9., 4., 5.],
#        [3., 4., 2., 5.]])

## concatenate 根据参数stack

视图(view)和浅复制

不同的数组对象分享同一个数据。视图方法创造一个新的数组对象指向同一数据。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

import numpy as np 

# 生成一个二维的数据
a = np.floor(10*np.random.random((3,4)))
# array([[2., 9., 5., 9.],
#        [5., 7., 3., 6.],
#        [3., 1., 9., 0.]])
c = a.view()
c is a 
# False
c.base is a 
# True
c.shape = 2,6 
array([[ 2., 9., 5., 9., 5., 7.],
       [ 3., 6.,  3., 1., 9., 0.]])
c.shape
# (2,6)
a.shape
# (3,4)
c[0,4] = 12
# array([[2., 9., 5., 9.],
#        [12., 7., 3., 6.],
#        [3., 1., 9., 0.]])

深复制

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

import numpy as np 

# 生成一个二维的数据
a = np.floor(10*np.random.random((3,4)))
# array([[2., 9., 5., 9.],
#        [5., 7., 3., 6.],
#        [3., 1., 9., 0.]])
d = a.copy()
d is a 
#　False
d.base is a
# False

常用方法总览

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

#1.创建数组
arange, array, copy, empty, empty_like, eye, fromfile, fromfunction, identity, linspace, logspace, mgrid, ogrid, ones, ones_like, r , zeros, zeros_like
#2.转换
astype, atleast 1d, atleast 2d, atleast 3d, mat 
#3.操作
array split, column stack, concatenate, diagonal, dsplit, dstack, hsplit, hstack, item, newaxis, ravel, repeat, reshape, resize, squeeze, swapaxes, take, transpose, vsplit, vstack 
#4.查询
all, any, nonzero, where 
#5.排序
argmax, argmin, argsort, max, min, ptp, searchsorted, sort 
#6.运算
choose, compress, cumprod, cumsum, inner, fill, imag, prod, put, putmask, real, sum 
#7.基本统计
cov, mean, std, var 
#8.线代运算
cross, dot, outer, svd, vdot

Numpy 进阶

线性代数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import numpy as np 
# 导入线性代数的库
from numpy import linalg as ll
a = np.array([[1.0, 2.0], [3.0, 4.0]])
# array([[1., 2.],
#        [3., 4.]])
a.transpose() # 转置 a.T
# array([[1., 3.],
#        [2., 4.]])
ll.inv(a)  # 矩阵求逆
# array([[-2. ,  1. ],
#        [ 1.5, -0.5]])
u = np.eye(2)  # 生成一个单位矩阵
# array([[1., 0.],
#        [0., 1.]])
j = np.array([[0.0, -1.0], [1.0, 0.0]])
# array([[ 0., -1.],
#        [ 1.,  0.]])
np.dot (j, j)  #矩阵乘法运算
# array([[-1.,  0.],
#        [ 0., -1.]])
np.trace(u) # trace
# 2.0
y = np.array([[5.], [7.]])
# array([[5.],
#        [7.]])
ll.solve(a, y)  #计算a*y的解
# array([[-3.],
#        [ 4.]])
ll.eig(j)  #向量的特征值和特征向量
# (array([0.+1.j, 0.-1.j]),
#  array([[0.70710678+0.        j, 0.70710678-0.        j],
#         [0.        -0.70710678j, 0.        +0.70710678j]]))

矩阵类

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

import numpy as np
A = np.matrix('1.0 2.0; 3.0 4.0')  ## 生成一个矩阵
# matrix([[1., 2.],
#         [3., 4.]])
type(A)
# numpy.matrixlib.defmatrix.matrix
A.T  ## transpose
# matrix([[1., 3.],
#         [2., 4.]])
X = np.matrix('5.0 7.0')
# matrix([[5., 7.]])
Y = X.transpose()  ## X.T
# matrix([[5.],
#         [7.]])
A*Y  ## 矩阵乘法，注意维度
# matrix([[19.],
#         [43.]])
A.I  ## inverse
# matrix([[-2. ,  1. ],
#         [ 1.5, -0.5]])
ll.solve(A, Y)  ## solve A*Y
# matrix([[-3.],
#         [ 4.]])

注意NumPy中数组和矩阵有些重要的区别。

NumPy提供了两个基本的对象：一个N维数组对象和一个通用函数对象。其它对象都是建构在它们之上 的。特别的，矩阵是继承自NumPy数组对象的二维数组对象。

对数组和矩阵，索引都必须包含合适的一个或多个这些组合：整数标量、省略号 (ellipses)、整数列表;布尔值，整数或布尔值构成的元组，和一个一维整数或布尔值数组。矩阵可以被用作矩阵的索引，但是通常需要数组、列表或者 其它形式来完成这个任务。

像平常在Python中一样，索引是从0开始的。传统上我们用矩形的行和列表示一个二维数组或矩阵，其中沿着0轴的方向被穿过的称作行，沿着1轴的方向被穿过的是列。

矩阵与二维数组的不同

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

import numpy as np
  
A = np.arange(12)
#array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])
A.shape = (3,4)
# A
# array([[ 0,  1,  2,  3],
#        [ 4,  5,  6,  7],
#        [ 8,  9, 10, 11]])
M = mat(A.copy())
# matrix([[ 0,  1,  2,  3],
#         [ 4,  5,  6,  7],
#         [ 8,  9, 10, 11]])
A[:,1]
# array([1, 5, 9])
A[:,1].shape
#(3,)
M[:,1]
# matrix([[1],
#         [5],
#         [9]])
(3, 1)

注意最后两个结果的不同。

对二维数组使用一个冒号产生一个一维数组，然而矩阵产生了一个二维矩阵。

广播法则(rule)

广播法则能使通用函数有意义地处理不具有相同形状的输入。

当两个数组的形状并不相同的时候，我们可以通过扩展数组的方法来实现相加、相减、相乘等操作，这种机制叫做广播

广播的原则：如果两个数组的后缘维度（trailing dimension，即从末尾开始算起的维度）的轴长度相符，或其中的一方的长度为1，则认为它们是广播兼容的。广播会在缺失和（或）长度为1的维度上进行。

这句话乃是理解广播的核心。广播主要发生在两种情况，一种是两个数组的维数不相等，但是它们的后缘维度的轴长相符，另外一种是有一方的长度为1。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

import numpy as np 
 
a = np.array([[ 0, 0, 0],
           [10,10,10],
           [20,20,20],
           [30,30,30]])
b = np.array([1,2,3])
print(a + b)
#######
# [[ 1  2  3]
#  [11 12 13]
#  [21 22 23]
#  [31 32 33]]

http://www.runoob.com/wp-content/uploads/2018/10/image0020619.gif

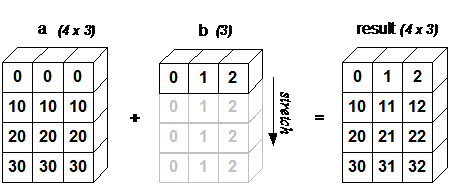
4x3 的二维数组与长为 3 的一维数组相加，等效于把数组 b 在二维上重复 4 次再运算。

广播的规则:

  • 让所有输入数组都向其中形状最长的数组看齐，形状中不足的部分都通过在前面加 1 补齐。
  • 输出数组的形状是输入数组形状的各个维度上的最大值。
  • 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时，这个数组能够用来计算，否则出错。
  • 当输入数组的某个维度的长度为 1 时，沿着此维度运算时都用此维度上的第一组值。

**简单理解：**对两个数组，分别比较他们的每一个维度（若其中一个数组没有当前维度则忽略），满足：

  • 数组拥有相同形状。
  • 当前维度的值相等。
  • 当前维度的值有一个是 1。

若条件不满足，抛出 “ValueError: frames are not aligned” 异常。

Numpy 陷阱

陷阱一：数据结构混乱

Numpy中的array和matrix结构比较混乱，在计算时如果不注意会出问题。

https://blog-1253453438.cos.ap-beijing.myqcloud.com/numpy/00.png

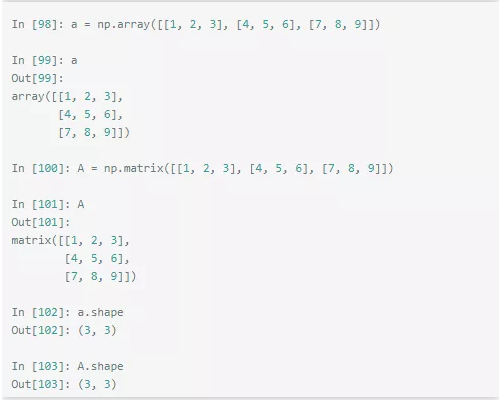
如上图所示，我们创建一个二维的数组和二维的矩阵。

https://blog-1253453438.cos.ap-beijing.myqcloud.com/numpy/01.png

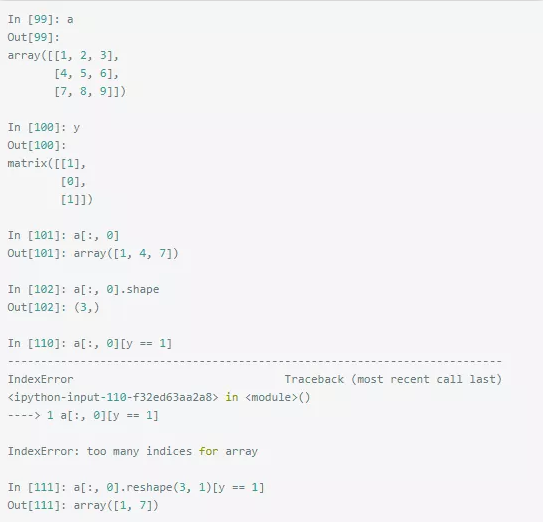
从 Out[101] 可以看到一个陷阱，a[:, 0] 过滤完应该是一个 3 x 1 的列向量，可是它变成了行向量。其实也不是真正意义上的行向量，因为行向量 shape 应该是 3 x 1，可是他的 shape 是 (3,) ，这其实已经退化为一个数组了。所以，导致最后 In [110] 出错。只有像 In [111] 那样 reshape 一下才可以。

相比之下，matrix 可以确保运算结果全部是二维的，结果相对好一点。

https://blog-1253453438.cos.ap-beijing.myqcloud.com/numpy/02.png

Out [114] 我们预期的输入结果应该是一个 2 x 1 的列向量，可是这里变成了 1 x 2 的行向量！

在矩阵运算里，行向量和列向量是不同的。比如一个 m x 3 的矩阵可以和 3 x 1 的列向量叉乘，结果是 m x 1 的列向量。而如果一个 m x 3 的矩阵和 1 x 3 的行向量叉乘是会报错的。

陷阱二：数据处理能力不足

假设 X 是 5 x 2 的矩阵，Y 是 5 X 1 的 bool 矩阵，我们想用 Y 来过滤 X ，即取出 Y 值为 True 的项的索引，拿这些索引去 X 里找出对应的行，再组合成一个新矩阵。

https://blog-1253453438.cos.ap-beijing.myqcloud.com/numpy/03.png

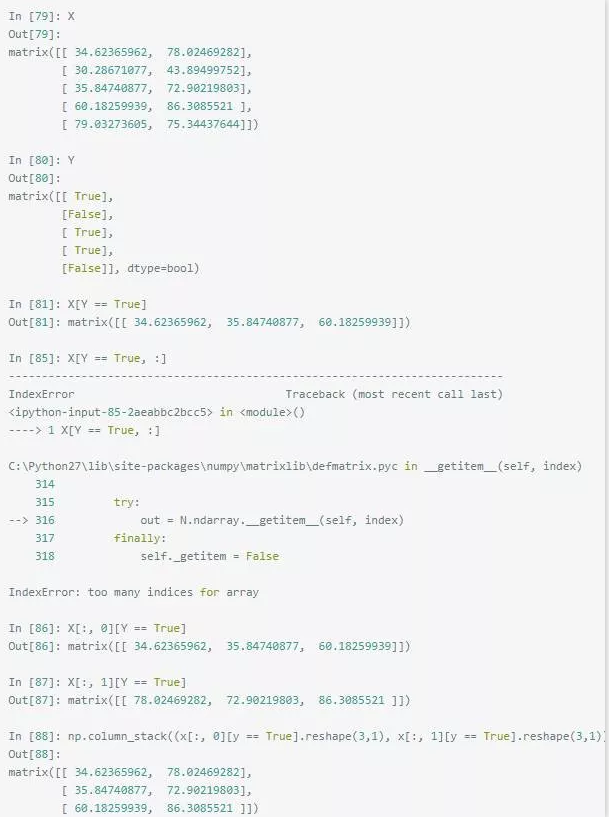
我们预期 X 过滤完是 3 x 2 列的矩阵，但不幸的是从 Out[81] 来看 numpy 这样过滤完只会保留第一列的数据，且把它转化成了行向量，即变成了 1 x 3 的行向量。不知道你有没有抓狂的感觉。如果按照 In [85] 的写法，还会报错。如果要正确地过滤不同的列，需要写成 In [86] 和 In [87] 的形式。但是即使写成 In [86] 和 In [87] 的样式，还是一样把列向量转化成了行向量。所以，要实现这个目的，得复杂到按照 In [88] 那样才能达到目的。实际上，这个还达不到目的，因为那里面写了好多硬编码的数字，要处理通用的过滤情况，还需要写个函数来实现。

陷阱三：数值运算句法混乱

在机器学习算法里，经常要做一些矩阵运算。有时候要做叉乘，有时候要做点乘。我们看一下 numpy 是如何满足这个需求的。

假设 x, y, theta 的值如下，我们要先让 x 和 y 点乘，再让结果与 theta 叉乘，最后的结果我们期望的是一个 5 x 1 的列向量。

https://blog-1253453438.cos.ap-beijing.myqcloud.com/numpy/04.png

https://blog-1253453438.cos.ap-beijing.myqcloud.com/numpy/05.png

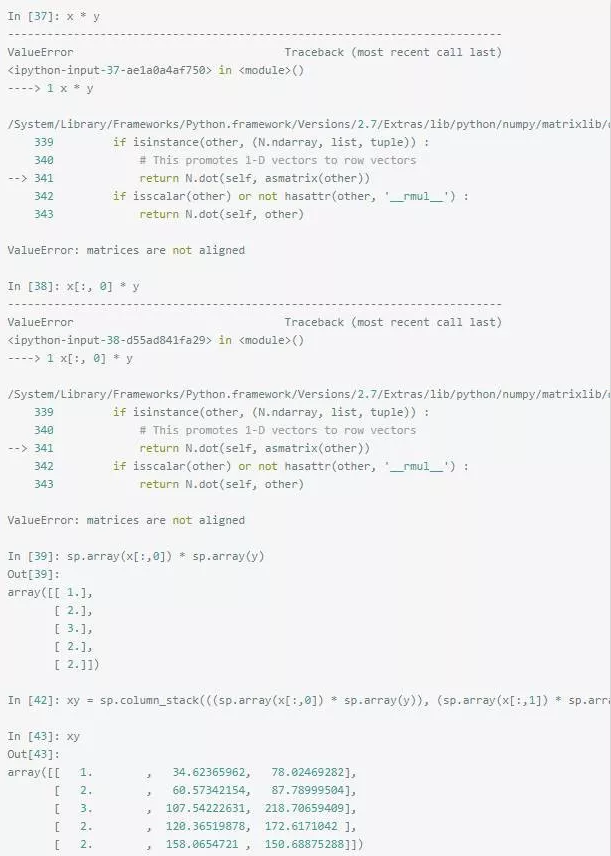
直观地讲，我们应该会想这样做：(x 点乘 y) 叉乘 theta。但很不幸，当你输入 x * y 时妥妥地报错。那好吧，我们这样做总行了吧，x[:, 0] * y 这样两个列向量就可以点乘了吧，不幸的还是不行，因为 numpy 认为这是 matrix，所以执行的是矩阵相乘（叉乘），要做点乘，必须转为 array 。

所以，我们需要象 In [39] 那样一列列转为 array 和 y 执行点乘，然后再组合回 5 x 3 的矩阵。好不容易算出了 x 和 y 的点乘了，终于可以和 theta 叉乘了。

https://blog-1253453438.cos.ap-beijing.myqcloud.com/numpy/06.png

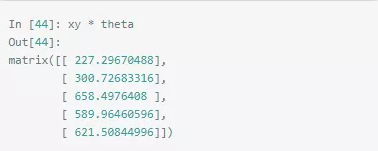
看起来结果还不错，但实际上这里面也是陷阱重重。

https://blog-1253453438.cos.ap-beijing.myqcloud.com/numpy/07.png

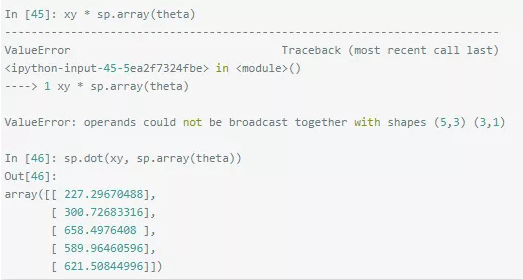
In [45] 会报错，因为在 array 里 * 运算符是点乘，而在 matrix 里 * 运算符是叉乘。如果要在 array 里算叉乘，需要用 dot 方法。看起来提供了灵活性，实际上增加了使用者的大脑负担。

如果想要避免array和matrix的点乘和叉乘，最好使用numpy提供的方法np.multiply（点乘）和np.dot（叉乘）；而不是使用默认的*****

参考链接

更新于 2018-12-25
 python, Numpy
返回 | 主页